Data
Structures – TREES
Previously studied Data Structures like Linked Lists or Arrays form the
linear structure but trees are the non – linear structures. Trees form the
hierarchical form of structure.
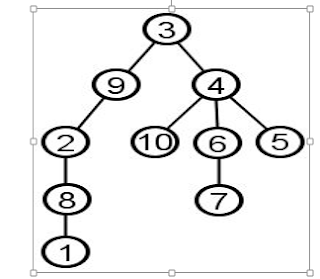
Representation of Tree in Computer Science–
If you cannot understand it now, it does not matter. You will
understand it in course of time.
Now, most of you must be wondering that WHY TREES??
Trees are important-
1. For faster
search, greater than linked lists but slower than arrays.
2. For faster insertion
and deletion, greater than arrays but slower than linked lists.
3. To represent the
relationship which contains hierarchy naturally like the family or the file
system of the computer.
Terminologies of Tree Data Structure –
1. Node – Each element in the tree form a node or is
called a node.
2. Edges – The connections connecting the nodes to
each other are called edges or
links or branches (for more tree
like feeling)
3. Child Node – The nodes connecting to a
node in downward position or the immediate
successors, we can say, are the node’s child node.
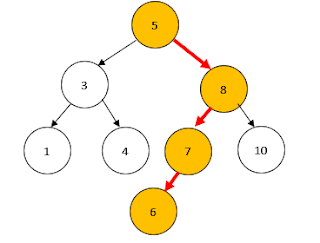
In above ex- The node 3, 8 are the child nodes of 5
but node 1, 4 or 7, 10 are not the
child nodes of 5 as they are not immediately connected rather they are termed
the grand- children of 5( child of
child). This continues like the real family terminology.
4. Parent Node – The nodes connecting to a
node in an upward position (if drawn in the above fashion) or the immediate predecessor
of the node are called the parent node of a node. For ex- 3 is the parent of
nodes 1 and 3, 8 is the parent node of 7 and 10 but 5 is the grandparent of nodes 1, 4, 7, 10.
5. Siblings – The nodes which have the
same parent are the siblings.
6. Root Node- The node which have no
parent is the root node.
7. Leaf nodes – Nodes which do not have
any children nodes are the leaf nodes or terminal
nodes or external nodes.
8. Internal Nodes – All the nodes which are
not the leaf node are the internal node or the interior node including the root itself.
9.
Degree of a node -The number of
nodes connected to a node with edges or links form the degree of a node. In
the topmost figure of tree
Degree(4) = 4 (3
children + 1 parent).
10.
Path- the path is a
sequence of nodes and edges connecting a node with a descendant. A path starts
from node and ends with another node or leaf.
Remember –
1. The path includes
all the nodes and edges coming in its way and not just edges.
2. The path is
moving downward and its direction cannot be changed in middle. For ex – there
cannot be any path from node 3 to node 6. Also, there cannot be any path from
leaf to the root.
11. Height of a node- The height of a node is
the number of edges on the longest
downward path between the node and the leaf. The path is always downward so
we can remove this redundant word from here.
Each node has height. 3 has
height and so does 8 and 7 and etc.
Leaf nodes have no height as
there cannot be any path from leaf
node to leaf node, so height of leaf
node =0.
Keep in mind, it is the
longest path so the height of node 5 is the path from node 5 to leaf node 6 and
not to any other node like 1, 4 or 7.
Height of a tree – The
height of a tree is the height of the root node itself.
12. Depth of a node- The depth of a node is the
number of edges from the node to the root node.
Depth of root
node is 0.
13. Level of a node- The level of a node is
defined as number of connections between the node and the root, or the distance
between the node and the root node, with root having level =0.
Ex-
5(root node) is at level 0,
3, 8 at level 1
1, 4, 7, 10 at level 2
14. Ancestor of a node – A node A is an ancestor
of B if some node A is a parent node of
B or if some child node of A is an ancestor node of B. Stating in simple terms,
node A is an ancestor of B if B is child of A or grand-child of A or child of
grand – child of A or so on. For ex – 5 is an ancestor of nodes 1, 4, 7, 10.
15. Descendant of a node – A node A is a descendant
of node B if it is child node of B or child of some child of node B. Stating in
simple terms, A node A is descendant of node B if B is ancestor of A. For ex-
1, 4, 7 ,10 , 5 ,8 all are descendants of node 5.
16. Forest- the forest, like you may think consist of
so many trees, it is same here in the computer science. The forest is made up
of n disjoint trees (independent trees) where n >=0.
For ex – if we remove node 5
than node 3 with children 1 and 4 and node 8 with children 7 and 10 form a
forest with n=2.
This the forest with two trees (n=2).
Types of Trees –
1 k-ary Trees – the node can have at most k
children.
2. Threaded trees – nodes point to their
successor or predecessor trough pointers.
3. B- Trees – more than one value can be
present in each node.
For more and better visual representations
check out our video - https://www.youtube.com/watch?v=FFOTq1RcrBE
Any Queries or updates or any problem in
document or the Video that you may want to discuss you can follow our twitter
account - https://twitter.com/Logic_Heap





No comments:
Post a Comment